Üçgende Açıortay ve Kenarortay Bağıntıları Ders Notları – Konu Anlatımı

ÜÇGENDE AÇIORTAY BAĞINTILARI

1. Açıortay

Herhangi bir açının ölçüsünü iki eş açıya bölen ışınlara açıortay denir.Yandaki şekilde AOB açısını iki eş açıya ayıran [OC ışınına açıortay denir.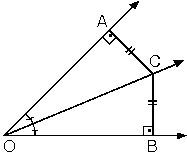

Açıortay üzerindeki herhangi bir noktadan açının kenarlarına çizilen dik uzunluklar eşittir.

AOB bir açı,

[OC açıortay

m(AOC) = m(COB)

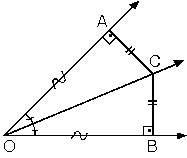
|AC| = |CB| AOC ve BOC eş üçgenler olduğundan |OA| = |OB|

2. İç Açıortay Bağıntısı

ABC üçgeninde [AN] açıortay ABN ve ANC üçgenlerinin[BC] tabanına göre, yükseklikleri eşit olduğundan olur …..(1)

ABN üçgeninde [AB] kenarına ait yükseklik ANC üçgeninde[AC] kenarına ait yüksekliğe eşittir. olur …..(2)

[AN] açıortay olmak şartıyla bu iki alan oranını birleştirirsek; (1) ve (2) den

olur

ABC üçgeninde [AN] açıortay olmak şartıyla Buradan ve b.y=c.x eşitlikleri de elde edilir.

3. İç Açıortay Uzunluğu

ABC üçgeninde A köşesinden çizdiğimiz açıortayuzunluğuna nAdersek

4. Dış Açıortay Bağıntısı

ABC üçgeninde [AD], A köşesine ait dış açıortaydır.

5. Dış Açıortay Uzunluğu

ABC üçgeninde [AD] dış açıortayının uzunluğunan’Adersek

6. İç açıortayla dış açıortay arasındaki açı

m(DAE)=90°

ABC üçgeninde [AD] iç açıortayı ile [AE] dış açıortayı arasındaki açı için

2a + 2b = 180°

a + b = 90° dir.

[DA] ^ [AE]

Bir üçgende iç açıortayların kesim noktası iç teğet çemberin merkezidir. P noktasının kenarlara uzaklığı eşittir. Merkezden indirilen dikmeler iç teğet çemberin yarıçapı olur.

• ÜÇGENDE KENARORTAY BAĞINTILARI

1. Ağırlık Merkezi

Üçgenlerde kenarortaylar bir noktada kesişirler.Kenarortayların kesişim noktasına ağırlık merkezi denir.

ABC üçgeninde [AD], [BE] ve [CF] kenarortaylarınınkesiştikleri G noktasına ABC üçgeninin ağırlık merkezidenir.

a. Ağırlık merkezi kenarortayı, kenara 1 birim, köşeye 2 birim olacak şekilde böler.

ABC üçgeninde D, E, F noktaları bulundukları kenarlarınorta noktaları ve G ağırlık merkezi ise eşitlikleri vardır.

b. Bir üçgende iki kenarortayın kesişmesiyle oluşan nokta ağırlık merkezidir.

c. ABC üçgeninde [AD] kenarortay ve|AG| = 2|GD| olduğundan G noktasıağırlık merkezidir.

d. ABC üçgeninde [AD] kenarortay ve |CG| = 2|FG|olduğundan G noktası ağırlık merkezidir.

e.ABC üçgeninde|AG| = 2|GD| ve |CG| = 2|GF|eşitliğini sağlayan G noktası ABC üçgeninin ağırlık merkezidir.

2. Dik üçgende hipotenüse ait kenarortay hipotenüsün yarısına eşittir.

ABC dik üçgeninde [BD] hipotenüse ait kenarortay |AG|=|DC|=|BD|

3. Kenarortayların Böldüğü Alanlar

a.Kenarortaylar üçgenin alanını altı eşit parçaya bölerler.

b.G ağırlık merkezi köşelere birleştirildiğinde üçgenin alanı üç eşit parçaya bölünür.

c. G ağırlık merkezi kenarların orta noktaları ile birleştirildiğinde üçgenin alanı üç eşit parçaya bölünür.

4.ABC üçgeninde kenarortaylar ve [FE] çizilirse|AK| = 3x|KG| = x |GD| = 2x eşitlikleri bulunur.

K noktası [AD] kenarortayının orta noktasıdır.

[FE] //[BC]

2[FE]=[BC]

a. ABC üçgeninde kenarortaylar ve [FE] çizildiğindeşekildeki gibi bir alan bölünmesi oluşur.

b.Kenarların orta noktalarını birbirine birleştirdiğimizde üçgenin alanı dört eşit parçaya bölünür.

5. Kenarortay Uzunluğu

ABC üçgeninde A köşesinden çizilenkenarortayın uzunluğuna Vadersek Bu bağıntı diğer kenarortaylar içinde geçerlidir.

Kenarortaylar taraf tarafa toplanırsa

Kenarortaylar taraf tarafa toplanırsa

6. Dik Üçgende Kenarortaylar

A açısı 90° olan bir dik üçgende kenarortaylar arasında